4.4.1. ESTABLECIMIENTO DE LA PRECISIÓN
Sea H
un intervalo cualquiera definido sobre la recta real. Definiremos ahora una
variable ficticia, XH, de la siguiente forma:

De
manera que cada observación de Xt Ileva asociada una observación -con valor o ó
1- de la variable XNr . La función de densidad teórica -desconocida- de Xt
asigna una probabilidad pH al intervalo H. Esto significa que:

Producir
T replicaciones del vector y, implica disponer de una muestra de T
“observaciones" de la variable real X. Esta muestra lleva asociada, a su
vez, una muestra de tamaño T de la variable Xy .Esta variable sigue una
distribución binaria de parámetro pH , así que la suma de las T observaciones
de XH , ZH = XH^ +. ,.+ X y T , sigue una distribución binomial b(pH ,^. Es
oportuno aquí hacer una adaptación al presente contexto del concepto de
estimación precisa de Finster (1987) Definición 1. ,ZH /T es una estimación
precisa de pN con nivel de imprecisión A y confianza 1-a (can 0< cx < 1),
si

El
conjunta de precisión [-A, A] es el conjunto de errores de simulación
aceptables. En lo que sigue a continuación se intentará determinar cuál es el
número de replicaciones mínimo para obtener una estimación de pH can nivel de
imprecisión fijo A y confianza 1-a. El teorema de Moivre (ver por ejemplo Fz.
de Trocóniz 1993) prueba que la sucesión b(pH ,1), b(pH ,2),. ..,b(pH , 7^, es
asintóticamente normal N{T pH ,T p^ [1- pH ]) de manera que si T pH > 1 S se
suele tomar como válida la siguiente aproximación a la distribución de
ZH:

entonces,
para la frecuencia binomial, ZH IT, se tiene :

Si t^
es el cuantil aJ2 correspondiente a la cola derecha de la distribución
N(0,1),

4.4.2.
CÁLCULO DEL NÚMERO MÍNIMO DE OBSERVACIONES NECESARIAS
El
tamaño de la muestra o cálculo de número de observaciones es un proceso vital
en la etapa de cronometraje, dado que de este depende en gran medida el nivel
de confianza del estudio de tiempos. Este proceso tiene como objetivo
determinar el valor del promedio representativo para cada elemento.
Los
métodos más utilizados para determinar el número de observaciones son:
- Método Estadístico
- Método Tradicional
Método estadístico
El método estadístico requiere que se efectúen cierto número de observaciones preliminares (n’), para luego poder aplicar la siguiente fórmula:
El método estadístico requiere que se efectúen cierto número de observaciones preliminares (n’), para luego poder aplicar la siguiente fórmula:
NIVEL
DE CONFIANZA DEL 95,45% Y UN MARGEN DE ERROR DE ± 5%

Siendo:
n =
Tamaño de la muestra que deseamos calcular (número de observaciones)
n’ =
Número de observaciones del estudio preliminar
Σ =
Suma de los valores
x =
Valor de las observaciones.
40 =
Constante para un nivel de confianza de 94,45%
Ejemplo:
Se
realizan 5 observaciones preliminares, los valores de los respectivos tiempos
transcurridos en centésimas de minuto son: 8, 7, 8, 8, 7. Ahora pasaremos a
calcular los cuadrados que nos pide la fórmula:
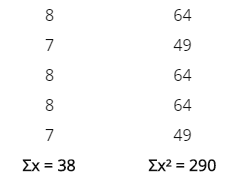
n’ = 5
Sustituyendo
estos valores en la fórmula anterior tendremos el valor de n:

Dado
que el número de observaciones preliminares (5) es inferior al requerido (7),
debe aumentarse el tamaño de las observaciones preliminares, luego recalcular
n. Puede ser que en recálculo se determine que la cantidad de 7 observaciones
sean suficientes.
Método
tradicional
Este
método consiste en seguir el siguiente procedimiento sistemático:
1. Realizar
una muestra tomando 10 lecturas sí los ciclos son <= 2 minutos y 5 lecturas
sí los ciclos son > 2 minutos, esto debido a que hay más confiabilidad en
tiempos más grandes, que en tiempos muy pequeños donde la probabilidad de error
puede aumentar.
2. Calcular
el rango o intervalo de los tiempos de ciclo, es decir, restar del tiempo mayor
el tiempo menor de la muestra:
R (Rango)
= Xmax – Xmin
3. Calcular
la media aritmética o promedio:

Siendo:
Σx =
Sumatoria de los tiempos de muestra
n =
Número de ciclos tomados
4. Hallar
el cociente entre rango y la media:

5. Buscar
ese cociente en la siguiente tabla, en la columna (R/X), se ubica el valor
correspondiente al número de muestras realizadas (5 o 10) y ahí se encuentra el
número de observaciones a realizar para obtener un nivel de confianza del 95% y
un nivel de precisión de ± 5%.

Ejemplo
Tomando
como base los tiempos contemplados en el ejemplo del método estadístico,
abordaremos el cálculo del número de observaciones según el método tradicional.
En
primer lugar como el ciclo es inferior a los 2 minutos, se realizan 5 muestras
adicionales (6, 8, 8, 7, 8) para cumplir con las 10 muestras para ciclos <=
2 minutos. Las observaciones son las siguientes:

Se
calcula el rango:
R (Rango)
= 8 – 6 = 2
Ahora
se calcula la media aritmética:

Ahora
calculamos el cociente entre el rango y la media:

Ahora
buscamos ese cociente en la tabla y buscamos su intersección con la columna de
10 observaciones:

Tenemos
entonces que el número de observaciones a realizar para tener un nivel de
confianza
del 95% según el método tradicional es: 11
Al
adicionar los 5 tiempos y utilizar el método estadístico tenemos un número de
observaciones igual a: 12.8 aproximadamente 13.
4.4.3.
INTERVALOS DE CONFIANZA
Un
intervalo de confianza es una técnica de estimación utilizada en inferencia
estadística que permite acotar un par o varios pares de valores, dentro de
los cuales se encontrará la estimación puntual buscada (con una
determinada probabilidad).
Un
intervalo de confianza nos va a permitir calcular dos valores alrededor de una
media muestral (uno superior y otro inferior). Estos valores van a acotar un
rango dentro del cual, con una determinada probabilidad, se va a localizar el
parámetro poblacional.
Intervalo
de confianza = media +- margen de error
Conocer
el verdadero poblacional, por lo general, suele ser algo muy complicado.
Pensemos en una población de 4 millones de personas. ¿Podríamos saber el gasto
medio en consumo por hogar de esa población? En principio sí. Simplemente
tendríamos que hacer una encuesta entre todos los hogares y calcular la media.
Sin embargo, seguir ese proceso sería tremendamente laborioso y complicaría
bastante el estudio.
Ante
situaciones así, se hace más factible seleccionar una muestra
estadística. Por ejemplo, 500 personas. Y sobre dicha muestra, calcular la
media. Aunque seguiríamos sin saber el verdadero valor poblacional, podríamos
suponer que este se va a situar cerca del valor muestral. A esa media le
sumamos el margen de error y tenemos un valor del intervalo de confianza. Por
otro lado, le restamos a la media ese margen de error y tendremos otro valor.
Entre esos dos valores estará la media poblacional.
En
conclusión, el intervalo de confianza no sirve para dar una estimación puntual
del parámetro poblacional, si nos va a servir para hacernos una idea aproximada
de cuál podría ser el verdadero de este. Nos permite acotar entre dos valores
en dónde se encontrará la media de la población.
Factores
de los que depende un intervalo de confianza
El
cálculo de un intervalo de confianza depende principalmente de los siguientes
factores:
- Tamaño de la muestra
seleccionada: Dependiendo de la cantidad de datos
que se hayan utilizado para calcular el valor muestral, este se acercará
más o menos al verdadero parámetro poblacional.
- Nivel de confianza: Nos
va a informar en qué porcentaje de casos nuestra estimación acierta. Los
niveles habituales son el 95% y el 99%.
- Margen de error de
nuestra estimación: Este se denomina como alfa y
nos informa de la probabilidad que existe de que el valor poblacional esté
fuera de nuestro intervalo.
- Lo estimado en la muestra (media, varianza, diferencia de medias…): De esto va a depender el estadístico pivote para el cálculo del intervalo.
4.5
MUESTRAS DEFINITIVAS
El
tamaño de la muestra definitiva para poblaciones infinitas se calcula a partir
de la proporcionalidad que guarda el coeficiente de error típico respecto a la
media de una muestra piloto previa, como antecedente de los datos de la
población; resultado de un coeficiente esperado u; y s, preliminares. Donde a
partir de la ecuación del coeficiente de error típico, se despeja n y
sustituyendo se obtiene:
Cuando
se trata de inferir proporciones (P) de una muestra definitiva, por intervalo
de confianza, a partir de datos preliminares, generalmente se usa:
P =
Proporción de la población,
p =
Proporción de la muestra,
Sp =
Desviación típica de proporciones de la muestra
La
muestra definitiva de una población desconocida, calculada para un error típico
de proporciones esperado e; a partir de una proporcionalidad preliminar;
despejando y sustituyendo para n, es:
La
muestra definitiva extraída de una población conocida, con un coeficiente de
error típico esperado u; a partir de xx y s, preliminares, se calcula de la
siguiente forma:
Para
proporciones y su variación:
4.5.1
ESTADÍSTICAS DESCRIPTIVAS
En la
estadística descriptiva se sustituye o reduce el conjunto de datos obtenidos
por un pequeño número de valores descriptivos, como pueden ser: el promedio, la
mediana, la media geométrica, la varianza, la desviación típica, etc. Estas
medidas descriptivas pueden ayudar a brindar las principales propiedades de los
datos observados, así como las características clave de los fenómenos bajo
investigación.
Por lo general, la información proporcionada por la
estadística descriptiva puede ser trasmitida con facilidad y eficacia mediante
una variedad de herramientas gráficas, como pueden ser:
Gráficos de tendencia: es un trazo de una característica de interés sobre un
periodo, para observar su comportamiento en el tiempo.
Gráfico de dispersión: ayuda al análisis de la relación entre dos
variables, representado gráficamente sobre el eje x y el correspondiente valor
de la otra sobre el eje y.
Histograma: describe
la distribución de los valores de una característica de interés.
Estos métodos gráficos son de mucha utilidad para
entender con claridad un fenómeno analizado. La evolución de la inflación, el
tipo de cambio, del PBI u otros indicadores macro pueden ser analizados, por
ejemplo, con gráficos de tendencia.
Así, la estadística descriptiva constituye un modo
relativamente sencillo y eficiente para resumir y caracterizar datos. También
ofrece una manera conveniente de presentar la información recopilada. Este método es potencialmente aplicable a todas las
situaciones que involucran el uso de datos. Además de ayudar en el análisis e
interpretación de los datos, constituye una valiosa ayuda en el proceso de toma
de decisiones.
4.5.2 MUESTRAS
PEQUEÑAS: PRUEBA DE KOLMOGÓROV-SMIRNOV PARA AJUSTE DE UNA DISTRIBUCIÓN DE
PROBABILIDADES CONTINUA HIPOTÉTICA
Prueba
Kolmogorov-Smirnov para una muestra: Es una prueba de bondad de
ajuste. Se emplea en una muestra independiente. El tipo de variable es
cuantitativa continua (debe ser medida en escala al menos ordinal). Esta prueba
responde a la pregunta: ¿Ajusta la distribución empírica de datos muestrales de
una variable ordinal o cuantitativa a una distribución teórica conocida? Esta
prueba no requiere que los datos sean agrupados, lo que permite que ésta haga
uso de toda la información del conjunto de datos. Puede utilizarse con muestras
de cualquier tamaño (mientras que la X2 requiere que las muestras tengan un
tamaño mínimo).
Hipótesis:
H0:
F(x) = FT(x) para toda x desde - ∞ hasta + ∞
H1:
F(x) ≠ FT(x) para al menos una x
Como
es una prueba de bondad de ajuste aquí interesa no rechazar la hipótesis nula,
es decir, interesa que el valor de p sea mayor de 0,05 para no rechazar la
hipótesis nula (queremos que p > 0,05).
Ejemplo:
Se
efectuaron mediciones del nivel de glucemia de 36 hombres adultos en ayuno, no
obesos y aparentemente sanos. Estas mediciones se muestran en la tabla que se
presenta. Se pretende saber si es posible concluir que tales datos no
pertenecen a una población que sigue una distribución normal, con una media de
80 y una desviación típica de 6. Emplee un α = 0,05.

Respuesta:
Supuestos:
La muestra disponible es una muestra aleatoria simple que se extrajo de una
población que sigue una distribución continua.
Hipótesis:
H0:
F(x) = FT(x) para toda x desde - ∞ hasta + ∞
H1:
F(x) ≠ FT(x) para al menos una x
(ejemplo en excel)



Las pruebas G son pruebas de significación estadística de razón de verosimilitud o de máxima verosimilitud que se utilizan cada vez más en situaciones en las que anteriormente se recomendaban las pruebas de ji cuadrado.
4.5.3 MUESTRAS
GRANDES: PRUEBA DE KARL PEARSON PARA AJUSTE DE UNA DISTRIBUCIÓN DE
PROBABILIDADES HIPOTÉTICA, DISCRETA O CONTINUA
La
prueba chi-cuadrado, también llamada Ji cuadrado (Χ2), se encuentra dentro de
las pruebas pertenecientes a la estadística descriptiva, concretamente la
estadística descriptiva aplicada al estudio de dos variables. Por su parte, la
estadística descriptiva se centra en extraer información sobre la muestra. En
cambio, la estadística inferencial extrae información sobre la población.
El
nombre de la prueba es propio de la distribución Chi-cuadrado de la
probabilidad en la que se basa. Esta prueba fue desarrollada en el año 1900 por
Karl Pearson.
La
prueba chi-cuadrado es una de las más conocidas y utilizadas para analizar
variables nominales o cualitativas, es decir, para determinar la existencia o
no de independencia entre dos variables. Que dos variables sean independientes
significa que no tienen relación, y que por lo tanto una no depende de la otra,
ni viceversa.
Así,
con el estudio de la independencia, se origina también un método para verificar
si las frecuencias observadas en cada categoría son compatibles con la
independencia entre ambas variables.
Para
evaluar la independencia entre las variables, se calculan los valores que
indicarían la independencia absoluta, lo que se denomina “frecuencias
esperadas”, comparándolos con las frecuencias de la muestra.
Como
es habitual, la hipótesis nula (H0) indica que ambas variables son
independientes, mientras que la hipótesis alternativa (H1) indica que las
variables tienen algún grado de asociación o relación.
Así,
como otras pruebas para el mismo fin, la prueba chi-cuadrado se utiliza para
ver el sentido de la correlación entre dos variables nominales o de un nivel
superior (por ejemplo, la podemos aplicar si queremos conocer si existe
relación entre el sexo [ser hombre o mujer] y la presencia de ansiedad [sí o
no]).
Para
determinar este tipo de relaciones, existe una tabla de frecuencias a consultar
(también para otras pruebas como por ejemplo el coeficiente Q de Yule).
Si las
frecuencias empíricas y las frecuencias teóricas o esperadas coinciden, entonces
no hay relación entre las variables, es decir, éstas son independientes. En
cambio, si coinciden, no son independientes (existe relación entre las
variables, por ejemplo entre X e Y).
(ejemplo en excel)
4.5.4
OTRAS PRUEBAS: ANDERSON DARLING Y PRUEBA G
Anderson-Darling:
El
estadístico Anderson-Darling mide qué tan bien siguen los datos una
distribución específica. Para un conjunto de datos y distribución en
particular, mientras mejor se ajuste la distribución a los datos, menor será
este estadístico. Por ejemplo, usted puede utilizar el estadístico de
Anderson-Darling para determinar si los datos cumplen el supuesto de normalidad
para una prueba t.
Las
hipótesis para la prueba de Anderson-Darling son:
- H0: Los datos siguen una
distribución especificada
- H1: Los datos no siguen
una distribución especificada
Utilice
el valor p correspondiente (si está disponible) para probar si los datos
provienen de la distribución elegida. Si el valor p es menor que un nivel
de significancia elegido (por lo general 0.05 o 0.10), entonces rechace la
hipótesis nula de que los datos provienen de esa distribución. Minitab no
siempre muestra un valor p para la prueba de Anderson-Darling, porque este
no existe matemáticamente para ciertos casos.
También
puede utilizar el estadístico de Anderson-Darling para comparar el ajuste de
varias distribuciones con el fin de determinar cuál es la mejor. Sin embargo,
para concluir que una distribución es la mejor, el estadístico de
Anderson-Darling debe ser sustancialmente menor que los demás. Cuando los
estadísticos están cercanos entre sí, se deben usar criterios adicionales, como
las gráficas de probabilidad, para elegir entre ellos.
Distribución
|
Anderson-Darling
|
Valor p
|
Exponencial
|
9.599
|
p
< 0.003
|
Normal
|
0.641
|
p
< 0.089
|
Weibull
de 3 parámetros
|
0.376
|
p
< 0.432
|

Exponencial

Normal

Weibull
de 3 parámetros
3
Ejemplo
de comparación de distribuciones
Estas
gráficas de probabilidad son para los mismos datos. Tanto la distribución
normal como la distribución de Weibull de 3 parámetros ofrecen un ajuste
adecuado a los datos.
Minitab
calcula el estadístico de Anderson-Darling usando la distancia al cuadrado
ponderada entre la línea ajustada de la gráfica de probabilidad (con base en la
distribución elegida y usando el método de estimación de máxima verosimilitud o
las estimaciones de mínimos cuadrados) y la función de paso no paramétrica. El
cálculo tiene mayor ponderación en las colas de la distribución.
Pruebas G:
Las pruebas G son pruebas de significación estadística de razón de verosimilitud o de máxima verosimilitud que se utilizan cada vez más en situaciones en las que anteriormente se recomendaban las pruebas de ji cuadrado.
La
fórmula general para G es:
dónde O> es el conteo observado en una celda, es el
recuento esperado bajo la hipótesis nula, denota
el logaritmo natural, y la suma se toma sobre todas las celdas no vacías.
Además, el recuento total observado debe ser igual al recuento total esperado:
dónde es
el número total de observaciones.
Las
pruebas G se han recomendado al menos desde la edición de 1981 de Biometry , un
libro de texto de estadísticas de Robert R. Sokal y F. James Rohlf.
Comentarios
Publicar un comentario